README_EN.md

comments	difficulty	edit_url	tags
true	Hard	https://github.com/doocs/leetcode/edit/main/solution/3500-3599/3515.Shortest%20Path%20in%20a%20Weighted%20Tree/README_EN.md	Tree Depth-First Search Binary Indexed Tree Segment Tree Array

3515. Shortest Path in a Weighted Tree

中文文档

Description

You are given an integer n and an undirected, weighted tree rooted at node 1 with n nodes numbered from 1 to n. This is represented by a 2D array edges of length n - 1, where edges[i] = [ui, vi, wi] indicates an undirected edge from node ui to vi with weight wi.

You are also given a 2D integer array queries of length q, where each queries[i] is either:

• [1, u, v, w'] – Update the weight of the edge between nodes u and v to w', where (u, v) is guaranteed to be an edge present in edges.
• [2, x] – Compute the shortest path distance from the root node 1 to node x.

Return an integer array answer, where answer[i] is the shortest path distance from node 1 to x for the ith query of [2, x].

 

Example 1:

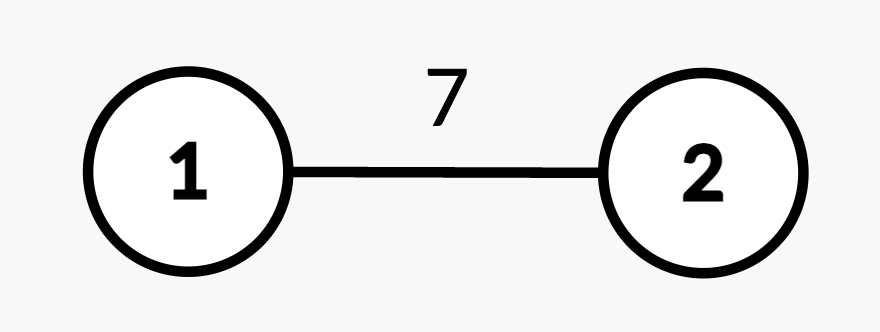
Input: n = 2, edges = [[1,2,7]], queries = [[2,2],[1,1,2,4],[2,2]]

Output: [7,4]

Explanation:

• Query [2,2]: The shortest path from root node 1 to node 2 is 7.
• Query [1,1,2,4]: The weight of edge (1,2) changes from 7 to 4.
• Query [2,2]: The shortest path from root node 1 to node 2 is 4.

Example 2:

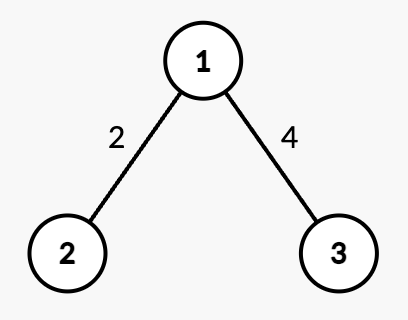
Input: n = 3, edges = [[1,2,2],[1,3,4]], queries = [[2,1],[2,3],[1,1,3,7],[2,2],[2,3]]

Output: [0,4,2,7]

Explanation:

• Query [2,1]: The shortest path from root node 1 to node 1 is 0.
• Query [2,3]: The shortest path from root node 1 to node 3 is 4.
• Query [1,1,3,7]: The weight of edge (1,3) changes from 4 to 7.
• Query [2,2]: The shortest path from root node 1 to node 2 is 2.
• Query [2,3]: The shortest path from root node 1 to node 3 is 7.

Example 3:

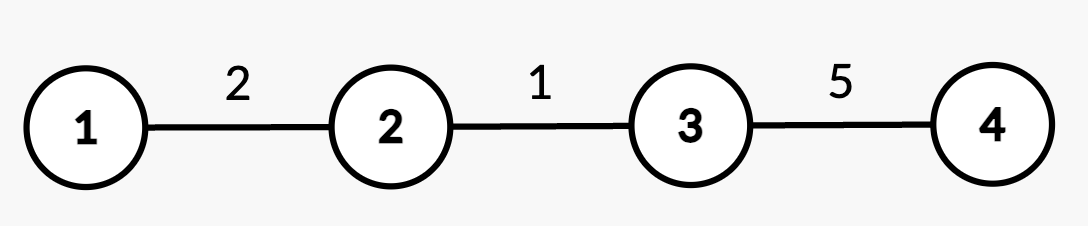
Input: n = 4, edges = [[1,2,2],[2,3,1],[3,4,5]], queries = [[2,4],[2,3],[1,2,3,3],[2,2],[2,3]]

Output: [8,3,2,5]

Explanation:

• Query [2,4]: The shortest path from root node 1 to node 4 consists of edges (1,2), (2,3), and (3,4) with weights 2 + 1 + 5 = 8.
• Query [2,3]: The shortest path from root node 1 to node 3 consists of edges (1,2) and (2,3) with weights 2 + 1 = 3.
• Query [1,2,3,3]: The weight of edge (2,3) changes from 1 to 3.
• Query [2,2]: The shortest path from root node 1 to node 2 is 2.
• Query [2,3]: The shortest path from root node 1 to node 3 consists of edges (1,2) and (2,3) with updated weights 2 + 3 = 5.

 

Constraints:

• 1 <= n <= 105
• edges.length == n - 1
• edges[i] == [ui, vi, wi]
• 1 <= ui, vi <= n
• 1 <= wi <= 104
• The input is generated such that edges represents a valid tree.
• 1 <= queries.length == q <= 105
• queries[i].length == 2 or 4
  • queries[i] == [1, u, v, w'] or,
  • queries[i] == [2, x]
  • 1 <= u, v, x <= n
  • (u, v) is always an edge from edges.
  • 1 <= w' <= 104

Solutions

Solution 1

Python3

Java

C++

Go